Classical Encryption Techniques
As we mentioned earlier, the basic of all encryption techniques are based on 2 techniques Substitution and Transposition and we can also use a combination of both of them.
Substitution is an encryption technique which elements in the plaintext are replaced or mapped with another elements.
There are many types of the substitution techniques such as Monoalphabetic Cipher and Polyalphabetic Cipher
We will drive an example of
monoalphabetic cipher called (Caesar cipher)
Caesar Cipher :
Is the simplest and the oldest known encryption techniques which elements in the plaintext are shifted with fixed number for example 3 places.

Example:
Plaintext: WELCOME TO CRYPTOGRAPHY
Ciphertext: ZHOFRPH WR FUBSWRJUDSKB
The ciphertext is produced by
adding 3 position for every letter.
As we can see here the encryption
algorithm for each plaintext P
shifted by 3 places to produces a ciphertext C= E(3,P) =
(P+3)mod26 so, generally the encryption algorithm for Caesar cipher is C= E(K,P) =(P+K)mod26
The decryption algorithm for Caesar cipher is P= D(K,C) = (C-K)mod26
Note: K takes a value from 1 to 25.Caesar cipher is too easy to break because it’s only uses 25 position keys, so simply try to preform a brute force using the 25 possible keys, and the language would help us in breaking this cipher. Nowadays in modern encryption we uses a very large keys such as 2048 bits or greater key long that gives us 2^2048 key space, it’s a very wide range of possible of keys.
Caesar cipher and many of substitution ciphers can be broken by using frequency of letters analysis.
It is a method to break a cipher encrypted by a substitution techniques.it is based on the relative of letters can be determined and compared to a standardfrequency distribution for a language.
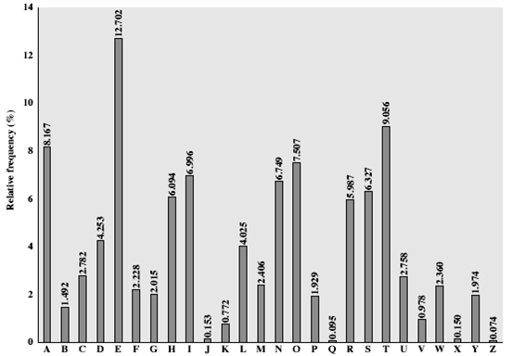
As we can see the previous figure , E is the most letter uses in English words by 12.7% , then T by 9.056% Or look at the next figure
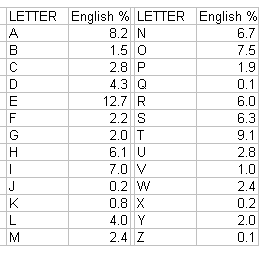
Example:
|
|
It’s a classic encryption technique , we try to apply the relative frequency analysis.

letter frequencies :
i : 58
e : 48
x : 41
w : 35
m : 34
v : 31
s : 30
r : 27
l : 22
p : 21
g : 16
h : 16
y : 13
t : 12
q : 12
c : 9
k : 9
j : 9
z : 6
f : 6
a : 5
o : 3
b : 2
u : 1
n : 1
d : 0
With these numbers and with some good guessing some words we can solve it.
I=e and L=H, X=t and E=a nd we get the following:
|
|
we can substitute V=r in “heVe” to be “here” and R=s in “Rtate” to be “state” ,M=i and Z=m from “atthattMZe” to be “atthattime”
we apply this change and get
|
|
We can deduce the substitution until we get a right message
|
|
After adding spaces
|
|
Note: Frequency of letters analysis works better as long as the cipher text is large.