Classical Encryption Techniques 2

Polyalphabetic Cipher is an encryption method to improve the simple substitution cipher techniques by using a larger key space and making the frequency of letters analysis harder.
Polyalphabetic Cipher is a block cipher with the following properties

1. The key space consists of all order of K = (k1, k2, k3, … ki) i= block length
2. Encryption of plaintext P = (p1, p2, p3 … pi)

Encryption algorithm
E(p+k) = (k1(p1).k2(p2).k3(p3).,,,, ki(pi))

Let’s drive an example of Polyalphabetic Cipher called Vigenère Cipher

Vigenère Cipher is Polyalphabetic Cipher technique and it’s uses 26 letters with shifting from 1 to 25 similar to Caesar Cipher but with a dynamic key which changes every time on i interval.
The encryption algorithm for Vigenère Cipher to produce a ciphertext C Ci = (Pi+Ki)

The decryption algorithm for Vigenère Cipher to produce a plaintext P Pi = (Ci-Ki)

Example:

Let key K= HAMZA and plaintext = WELCOME TO CRYPTOGRAPHY

key= HAMZAHAMZAHAMZAHAMZAH
Plaintext =  WELCOMETOCRYPTOGRAPHY
ciphertext =   ZEUBOTEFNCYYBSONRMOHF

simply we do addition operation on each element or by using the next table.

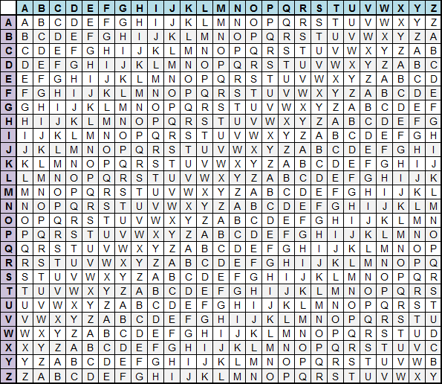
Ci = (Pi+Ki)

Note: If we look at letter frequencies

We reduced the frequency of letters analysis.

Vernam Cipher works on binary data rather than letters, that give us a defense against frequency letters analysis because there is no statistical relationship between the plaintext and the ciphertext.
The encryption algorithm in Vernam Cipher can be expressed as
Ci = Pi ⊕ Ki
Ci= ith binary digit of ciphertext.
Pi = ith binary digit of plaintext.
⊕ = exclusive-OR (XOR) operation.
Ki = ith binary digit of key.

The decryption algorithm in Vernam Cipher
Pi = Ci ⊕ Ki

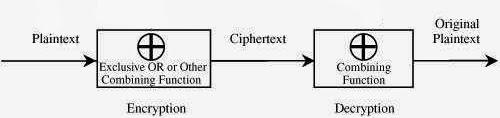
This system works by constructing a loop that takes the plaintext and the generated key bit by bit and preform XOR operation on each bit and then generate a ciphertext and so on to the end of the plaintext.

Now we have an important concept called “Prefect Secrecy”.

For any encryption algorithm has a perfect secrecy when the ciphertext gives us nothing about the plaintext(such as One-Time pad).

One-Time Pad is an encryption technique and it is UNBREAKABLE, by using a secret key as long as the plaintext, so the key will not repeated to fit the plaintext.
The key generator algorithm generates a key for each plaintext.
The secret key will be used to encrypt and decrypt for only one plaintext then the secret key will be destroyed.
The ciphertext has no statistical relationship to the plaintext , so this technique is UNBREAKABLE.

For Example
Suppose we use Vernam Cipher but with One-Time Pad method, we we generate a secret key as long as the plaintext and only for this plaintext.
Let’s try to encrypt “HELLO”
Plaintext  = HELLO
Secret key = XMCKL
by adding the values of each digit
Ciphertext = EQNVZ
If we try to crack the cipher without the secret key , and only one key can gives us the original plaintext we will get a lot of plaintexts, if we use exhaustive search we could translate this ciphertext into many plaintext, for example here we used the secret key = XMCKL , but if we use a secret key = TQURI on the same ciphertext = EQNVZ that gives us plaintext = LATER but ONLY ONE KEY IS THE RIGHT KEY.

Why One-Time Pad has a perfect secrecy?
Because of the randomness on keys and only one key use for one message(plaintext) and one ciphertext can be translated into many plaintext of same length, that makes the ciphertext gives us nothing about the plaintext.