AES
AES takes a plaintext block 16 bytes (128 bits) and key length 16, 24, 32 bytes (128, 192, 256 bits) AES-128, AES-192, AES-256 depending on key length.
The input to encryption or decryption algorithm in AES is 128 bits block = 16 bytes as 4x4 matrix, this matrix is copied into a state array, then the state array passes through and modified in each stage and then the state array is copied to output matrix.
The algorithm consists of N rounds, and N depends on key length
For 16 bytes key N=10 rounds
For 24 bytes key N=12 rounds
For 32 bytes key N=14 rounds
Initial transformation(Round 0) consists of add round key.
All rounds (except the final round) consists of 4 functions
- Substitute Bytes
- Shift Row
- Mix Column
- Add round key
The final round consists of 3 functions:
- Substitute Bytes
- Shift Row
- Add round key
AES in not a Feistel structure because in Feistel half of data is used to modify the other half and then the two halves are swapped, but AES processes the entire block.
The input key is expanded to 44 words 33 bits each, and every 4 words(128 bits) serve as input to each round
Substitute Bytes Transformation maps each state into a new value by a table look up process from S-Box table.
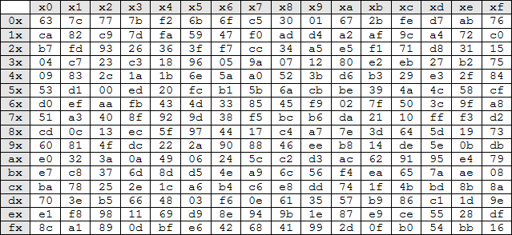
S-Box table is 16x16 matrix that contain a permutation of all possible 8-bits value by the following rules:
- The leftmost 4 bits are used as row value.
- The rightmost 4 bits are used as column value.
- The intersection to select a unique 8-bits value in S-Box.
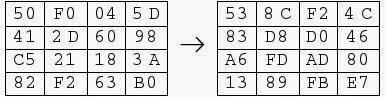
For example:
6A references row=6 column=A of S-Box which contain 02.
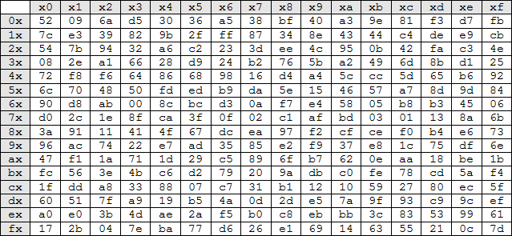
The inverse of Substitute Byts(InvSubBytes) is the same but we look up in inverse S-Box table instead of S-Box.
Shift Row Transformation apply the following on the state:
1. The first row is not altered.
2. The second row preform 1-byte circular left shift.
3. The third row preform 2-byte circular left shift.
4. The fourth row preform 3-byte circular left shift.
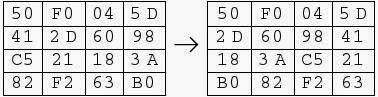
The inverse shift row(InvShiftRow) preform a circular shift to the right.
Mix Column Transformation operate on each column individually, each byte of a column is mapped into a new value that is a function of all four bytes in that column.
Mix column can be defined by the next multiplication on state.


For example:
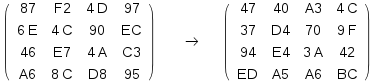
The inverse min column called(Inv MixColumn) is defined byNote: Dot notation refers to a multiplication in Galois field \({2}^{8}\)

Add round key Transformation preform XOR operation between the round key and state each 128 bits.
The randomness and round key expansion increase the security of AES.

What is key expansion?
The key expansion algorithm takes as input 16 bytes(4 words) and output 176 bytes(44 words) 4 words for each round and 4 words for initial add round key.
AES key expansion preform the next steps:
- Use input key in the first 4 words (w0,w1,w2,w3).
- Use the last word in each stage (w3,w7,w11,…) and preform one-byte shift left on the word
For example :
In stage one use w3(A,B,C,D)
After one-byte shift left
w3=(B,C,D,A) - Preform byte-substitution on each byte in word from S-box.
- XOR with the round constant word, the round constant word is a word which the three right most bytes are zeros in all rounds.
\(Rcon(i) = Rcon ,0,0,0\) which i=number of rounds
In
\(Rcon(1) = 01000000\)
\(Rcon(j) = 2.Rcon(j-1)\)
Note: The multiplication here in under Galois Field GF(\({2}^{8}\)
For example:
This is the input to AES 0F1571C947D9E8590CD7ADD6AF7F6798
W0 = 0F1571C9
W1 = 47D9E859
W2 = 0CD7ADD6
W3 = AF7F6798
Then we take the last word and preform key expansion- Preform one-byte shift left = 7F6798AF
- preform byte-substitution = D2854679
- Rcon for the first round = 01000000
- XOR D2854679 and 01000000
x1=D3854679
w4 = w0 \(\oplus\) x1= DC9037B0
w5 = w1 \(\oplus\) w4 = 9B49DFE9
w6 = w5 \(\oplus\) w2 = 97FE723F
w7 = w6 \(\oplus\) w3 = 388115A7