Simplified AES

Simplified AES is an educational algorithm to understand AES encryption algorithm , Simplified AES has the exact same structure of AES but with smaller parameters.
Simplified AES takes 16 bits input block, 16 bits key and produces 16 bits output block cipher.

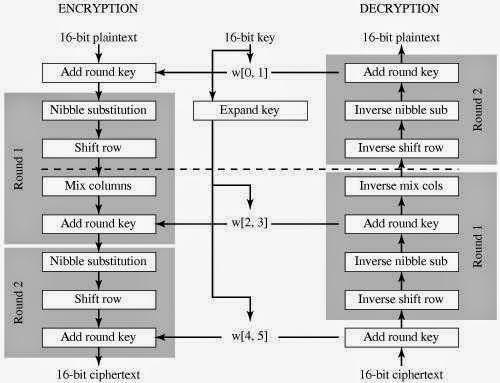
Simplified AES encryption algorithm uses 4 different functions transformations

1. Add key
2. Nibble substitution
3. Shift row
4. Mix column

Encryption algorithm itself consists of 3 rounds and each round contains functions

Round 1 –> Add key
Round 2 –> Nibble substitution –> Shift row –> Mix column –> Add key
Round 3 –> Nibble substitution –> Shift row –> Add key

As you can see in each round includes the add key function and make use of 16 bits key from the initial 16 bits key which expanded to 48 bits so each round can take 16 bits key(round key) to work with.
Each function operates on 16 bits as 2x2 matrix ordered in matrix by column, the first 8 bits of 16 bits of plaintext takes the first column and the second 8 bits takes the second column.
Now let’s look at each function individually

Add key function is operates XOR of 16 bits state matrix and 16 bits round key.

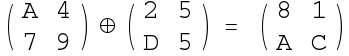
Substitution function maps each state into a new value by look up in S-Box table , this table contain all permutation of all 2^4 values by the following rules:

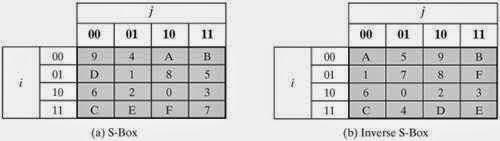
• The leftmost 2 bits are used as row value.
• The rightmost 2 bits are used as column value.
• The intersection selects a unique value in S-Box.
  For example :
  

Shift row function preforms one circular shift on the second row in state matrix.
For example :

Mix column function operates on each column individually, each value in column is mapped into a new value that is a function of both values in column.
The transformation as in the following matrix multiplication:

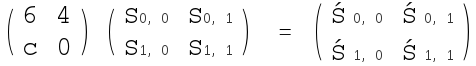
Then we get :

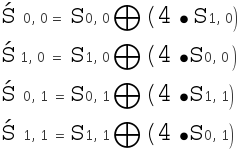
Note: Dot notation here refers to multiplication in GF(2^4).

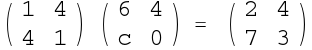
The initial 16 bits key split into 2 words each of 8 bits (W0 and W1) and expanded to six words(3 keys)
W2 = W0 ⊕ Rcon(1) ⊕ Sub(W1)
W3 = W2 ⊕ W1
W4 = W2 ⊕ Rcon(2) ⊕ Sub(w3)
W5 = W4 ⊕ W3

Sub: preform a substitution from S-box
Rcon: is Round constant so \(Rcon(i) = {x}^{i+2}\) to form the leftmost digits and the rest fill with zero
\(Rcon(1) = {x}^{3} = 1000\)
\(Rcon(2) = {x}^{4} mod({x}^{4+x+1}) = (x+1) = 0011\)