Block Cipher

Block cipher is an encryption method which the encryption algorithm operates on a plaintext block of n bits and produces a block of n bits ciphertext.
Block Cipher has \({2}^{n}\) possible different plaintext block to encrypt.

Nonsingular Transformation mean the encryption algorithm must be reversible (Nonsingular) to decrypt the ciphertext into the original plaintext.
The ciphertext must be unique for each plaintext block.
Example: Encryption block cipher with a plaintext block length n=4 bits and ciphertext, with \({2}^{4}=16\) possible input states

plaintext | Ciphertext    
0000         0101
0001         0111
0010         1001
0011         0000
0100         1100
0101         0110
0110         1010
0111         0011
1000         1011
1001         1000
1010         0010
1011         1111
1100         1110
1101         0001
1110         0100
1111         1101

This example has 16 possible input states, with a Nonsingular transformation as you can see in the next table

Ciphertext  |  Plaintext
0000            0011
0001            1101
0010            1010
0011            0111
0100            1110
0101            0000
0110            0101
0111            0001
1000            1001
1001            0010
1010            0110
1011            1000
1100            0100
1101            1111
1110            1100
1111            1011

As we can see this algorithm is reversible (Nonsingular).
There is a problem with a small block size n that this system is vulnerable to statistical analysis, but if n is large enough so the statistical analysis will be much harder.
Also it is not practical to establish a large enough reversible substitution cipher (The ideal block cipher), the solution of this problem is Feistel Cipher.

Feistel proposed that we can approximate the ideal block cipher system for large n ,built up by components that are easily realizable, which is the execution of 2 or more simple cipher in sequence and the result is a strong encryption.
The required form this approach is to develop a block cipher with a key length = k bits, and a block length = n bits with a total possible transformation = \({2}^{k}\) rather than \({2}^{n}\).

Feistel Cipher consists of a number of identical rounds of processing, and in each round a substitution is preformed on one half of data being processed followed by a permutation that make interchange the two halves.
The original key is expanded so that a different key is used for each round.

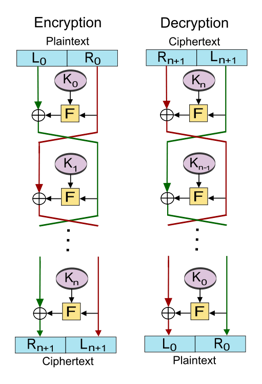
Feistel encryption algorithm(at the left hand side), the inputs to encryption algorithm are plaintext block of length 2w bits, and key K.
The plaintext is divided into two halves \({L}_{o}\) and \({R}_{o}\), passes through n rounds of processing, each round i has inputs \({L}_{i}-1\) and \({R}_{i}-1\), and then combined to produce the ciphertext block.
The subkey \({K}_{i}\) is derived from the overall \(K\), \({K}_{i}\) is different from \(K\) and from each other.

Feistel Cipher actually performs two operations
1- Substitution is performed on the left half of data by applying a round function F to the right half of data, then by doing XOR the output of round function F with the left half of data.
The round function F has the same structure every round but there is a change in parameter subkey \({K}_{i}\) for each round.
2- Permutation is performed that consists of interchange on the two halves of data.
Feistel Cipher structure is form of substitution permutation network (SPN).

Feistel Decryption Algorithm(at the right hand side), the inputs to decryption algorithm are ciphertext and subkey \({K}_{i}\) but in reverse order, start with \({K}_{n}\) then \({K}_{n}-1\) and so on until \({K}_{1}\) in the last round.

Note 1: At every round the value of encryption algorithm is equal to the corresponding value(n-ith) of decryption algorithm, but the two halves are swapped.
For example: For a system with 16 rounds, the  value of 5th round in encryption algorithm is equal to the value of 12th round of decryption algorithm, but L and R are swapped.
Note 2: The round function F does not required to be a reversible function.

1. Block size: Large block size mean greater security but reduced encryption and decryption speed.
2. Key size: Large key size mean greater security but may also reduced the encryption and decryption speed.
3. Number of rounds: Increasing security can be achieved by increasing the number of rounds.
4. Round Function F:  Increasing the complexity of round function F increasing the resistance to cryptanalysis.
5. Subkey generation algorithm: Increasing of complexity here also increasing the resistance to cryptanalysis.