DES

DES adopted in 1977 by (NIST) National Institute of Slandered and Technology.
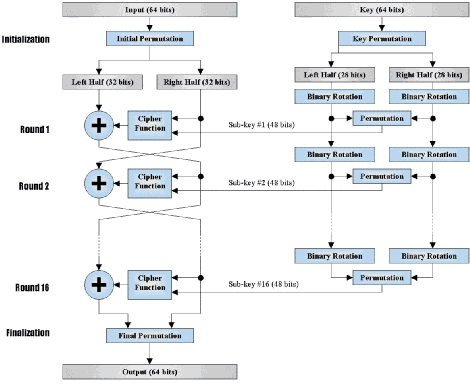
In DES data are encrypted in 64 bit block with a key length 56 bits and with output ciphertext 64 bits.
DES has the exact structure of Feistel Cipher but without Initial Permutation (IP) and Inverse Initial Permutation \(IP^{-1}\).

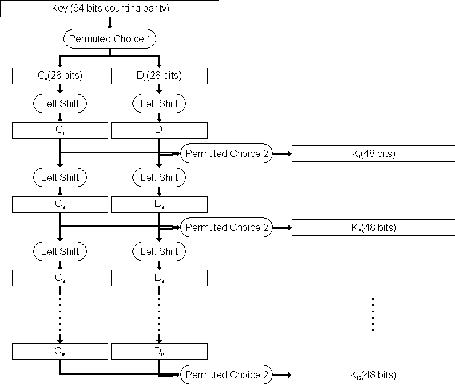
The key generator passes through many steps to produces subkeys.

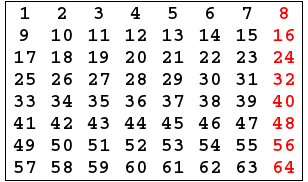
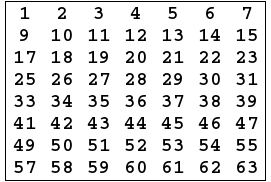
1. Key generator algorithm take 64 bits key as input,the input key numbered in a table from 1 to 64 as the following:
   
2. Every eighth bit is ignored and produce 56 bits.
   
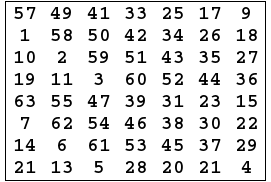
3. 56 bits passes through a permutation Choice one(PC-1)as the following:
   
4. The output is separated into two 28 bits C and D , the first 28 bits are called  \({C}_{0}\)(left part) and the last 28 bits are called \({D}_{0}\).
5. At each round a circular left shift is preformed on  \({C}_{i}-1\) and  \({D}_{i}-1\) by 1 or 2 bits by the next table.
   
6. Then \({C}_{i}-1\) and  \({D}_{i}-1\) in each round passes through permutation choice two (PC-2) to produces 48 bits.
   
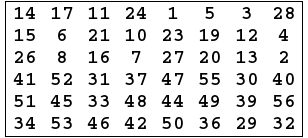
7. The permutation Choice Two output in each round is use as input to encryption algorithm.

There are two inputs to encryption algorithm Plaintext 64 bits and Encryption key 48 bits.
Encryption algorithm also passes through many steps to produce a ciphertext, The next figure

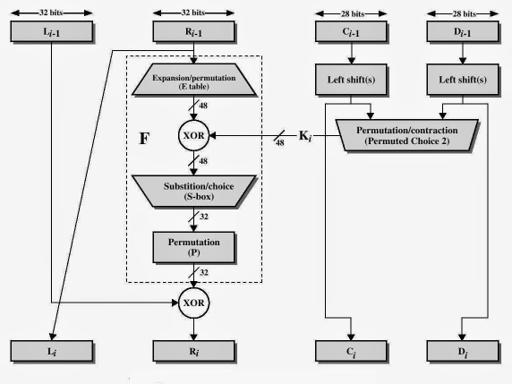
1. The plaintext block 64 bits pass through an initial permutation (IP) that rearranged bits and produces the permuted input.

• Initial Permutation takes the plaintext as input table consists of 64 bits numbered from 1 to 64
  
• Then the initial permutation will be permuted input 64 bits as the following:
  
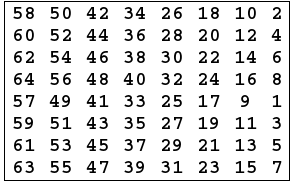
• The Inverse Initial Permutation is:
  

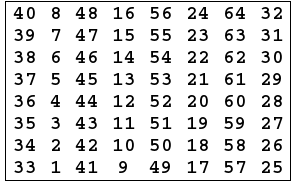
2. The permuted input block split into two halves each is 32 bits, the first 32 bits are called L and the last 32 bits are called R.
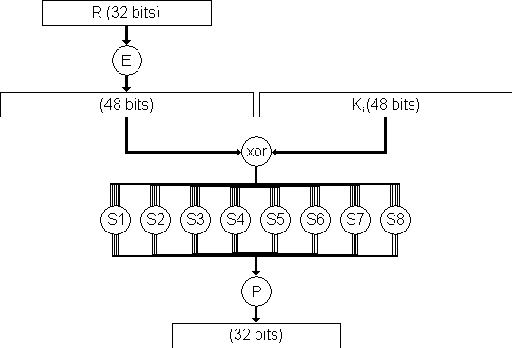
   Now The F function will start by the rest of all steps.

3. Expand R 32 bits to 48 bits to fit the subkey by preform Expansion permutation(E) as the following:
   

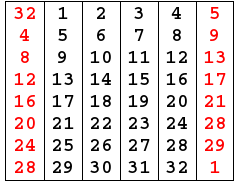
4. Preform Exclusive-OR between the subkey and Expansion Permutation (E) on R.
   E(\({R}_{i}\)-1)⊕ \({K}_{i}\).

5. The result of E(\({R}_{i}\)-1)⊕ \({K}_{i}\) pass through a substitution function and produces 32 bits output

Substitution Function is rolled by S-Box , S-Box consists of 8 boxes each of which accepts 6 bits as input and produces 4 bits output by the following:

1. Break the result of E(\({R}_{i}\)-1)⊕ \({K}_{i}\) into 8 blocks each contain 6 bits, These blocks are numbered from 1 to 8.
2. Each block will perform a substitution with S-Box with the same number by the following roles :
   

• The first and the last bits of each block together as 2 bit value to indicate the number of row in the same number S-Box.
• The middle four bits of each block together as-bit value to indicate the number of column in the same number S-Box.
• The decimal value which selected by the row and the column converted to-bit value in all S-Boxes.
  For Example:
  Suppose the first 6 bits of the result of E(\({R}_{i}\)-1)⊕ \({K}_{i}\) = 010101.
  So, the input to \({S}_{1}\) = 010101.
  The row value = 0 1 = 1 (decimal).
  The column value = 1010 = 10 (decimal).
  The decimal value will be 12 = 1100 (4 bit value).
• Combine results of each S-Box together 32 bits.

6. The result of the substitution operation (output of S-Boxes) passes through a Permutation Function (P).
   
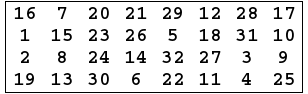
   At this point the function F is finished.
7. Perform Exclusive-OR between the output of the Permutation Function(P) and \({L}_{i}-1\)  , and then put the result in \({R}_{i}\) , and put \({R}_{i}-1\) in \({L}_{i}\).
   The overall formulas for DES Encryption Algorithm.
   \({L}_{i}\) = \({R}_{i}-1\). \({R}_{i}\) = \({L}_{i}-1\) ⊕ F(\({R}_{i}-1\),\({K}_{i}\)).
8. Perform 32-bit swap on the result of the final round , then perform Inverse Initial Permutation(\({IP}^{-1}\)) on the swapped data to produces the ciphertext 64 bits.

The inputs to decryption algorithm are ciphertext and subkey \({K}_{i}\) but in reverse order, start with \({K}_{n}\) then \({K}_{(n-1)}\) and so on until \({K}_{1}\) in the last round.

Note: You can use DES-Calculator to study each round in detail.